Leetcode 169 - majority element:

If you would rather learn visually, watch the video here --> youtu.be/enVivn6eXJY

Understand the problem

Leetcode 169 - majority element: Given an array nums of size n, return the majority element.

The majority element is the element that appears more than ( n / 2 ) times. You may assume that the majority element always exists in the array.

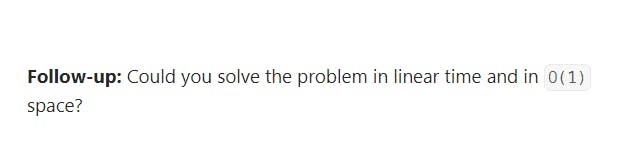
Follow-up: Could you solve the problem in linear time and in O(1) space?

We are given an array of integers
The majority element is the element that occurs more times than half the length of the array

This means that if the length of an array is 7; half the length of the array is ( 7 // 2 ) = 3 The majority element has to occur more than 3 times

Brute force approach

The brute force approach can be solved using the storage technique

Algorithm:

Loop over the items in the array
Then keep track of each item and the number of occurrences --- either in an object or hashmap
Return the item with the most occurrence

using map

const majorityElement = function(nums) {
const map = new Map()
let [maxCount, res] = [0, 0]

  for(let i = 0; i < nums.length; i++){
      map.set(nums[i], map.get(nums[i]) + 1 || 1)

      if(map.get(nums[i]) > maxCount){
          res = nums[i]
          maxCount = map.get(nums[i])
      } 
  }  

  return res
};

using object

const majorityElement = function(nums) {
    const obj = {}
    let [res, maxCount] = [0, 0]

    for(let i = 0; i < nums.length; i++){
        obj[nums[i]] = obj[nums[i]] + 1 || 1

        if(obj[nums[i]] > maxCount){
            res = nums[i]
            maxCount = obj[nums[i]]
        }
    }
    return res
};

Complexity Analysis

Time complexity: The time complexity of the storage technique is linear 0(n); this is because the code will run for the entire input size given, and the solution will run as large as the input size.

Space complexity: The space complexity is linear 0(n), the storage technique uses an extra data structure which can also grow as large as the input size

Follow up

We have a follow-up: can we solve this problem in constant space?

There are a number of techniques that can be used to accomplish this feat - none of them come intuitively - and some of them include divide and conquer, bit manipulation, boyer Moore's algorithm etc.

In this article, we will look at boyer Moore's algorithm.

Boyer Moore's algorithm

According to Wikipedia;

The Boyer–Moore majority vote algorithm is an algorithm for finding the majority of a sequence of elements using linear time and constant space. It is named after Robert S. Boyer and J Strother Moore, who published it in 1981,[1] and is a prototypical example of a streaming algorithm.

The algorithm is also written as this:

Initialise a variable for element m and a counter variable

For each element x

If the counter is 0

then the element m = element x

otherwise:

if element x == element m:

increment the counter

decrement the counter

return element m

Make it make sense, please...

The algorithm follows the survival of the fittest logic.

Let's examine the code sample below of an array with integers where at least one of them is a majority element:

[2,2,1,1,1,2,2]

Boyer Moore's method asks that we initialize two variables; m and counter - the m represents the majority element and the counter represents the number of times it has occurred.

At the start of the operation, they are initialized to 0

let [m, counter] = [0, 0]

Next, we loop over the given elements in the array. If the counter is equal to 0, the current value during iteration becomes the majority element and we store it in the variable m. This is the assumption the algorithm follows.

let [m, counter] = [0, 0]

for (let num of nums){
    if (counter === 0){
        m = num
    }
}

Outside of the conditional, we make the following check:

is the value in the m variable the same as the value in num;
- if it is, we increment the counter by 1
- else, we decrement the counter by 1

This statement can be translated into this code;

if (num  === m) counter += 1
else counter += -1

Or, we can use the ternary operator to simplify it:

counter += num === m ?  1 : - 1

Now, let's bring our code together

let [m, counter] = [0, 0]

for (let num of nums){
    if (counter === 0){
        m = num
    }
counter += num === m ?  1 : - 1
}

Continuing with our code analysis. On the first iteration; the element in our loop is 2

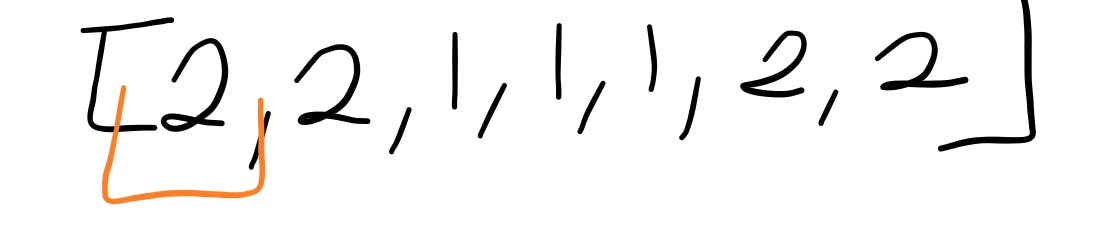
so we run through our algorithm quickly:

is counter === 0; yes it is
- since the counter is 0, the current element becomes the majority element
- m = 2
is the value of m the same as the current element in the iteration
- yes; m = 2, while current num = 2
- so, go ahead and increment the counter variable

And our most occurring element and counter are 2 and 1 respectively

m = 2, counter = 1

We move over to the next element in our iteration - 2

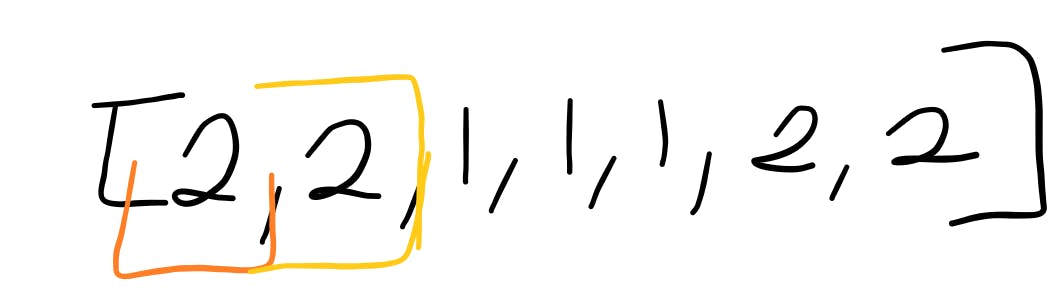
Algorithm:

is counter === 0; no it's not, it's 1
is the value of m the same as the current element in the iteration
- yes; they are both 2
- so, go ahead and increment the counter variable

m = 2, counter = 2

Next element in the iteration - 1

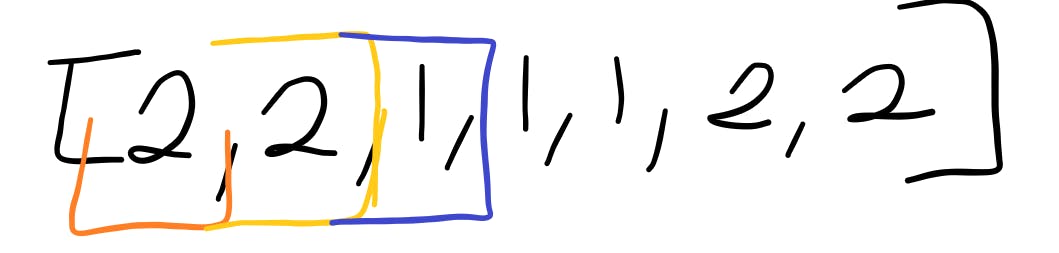
Algorithm:

is counter === 0; no it's not, it's 2
is the value of m the same as the current element in the iteration
- no; m = 2, while current num = 1
- so, go ahead and decrement the counter variable

m = 2, counter = 1

Next element in the iteration - 1

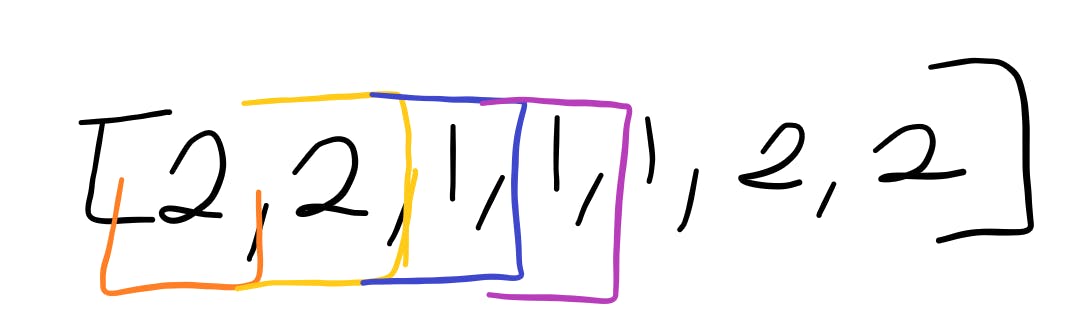
Algorithm:

is counter === 0; no it's not, it's 1
is the value of m the same as the current element in the iteration
- no; m = 2, while current num = 1
- so, go ahead and decrement the counter variable

m = 2, counter = 0

Next element in the iteration - 1

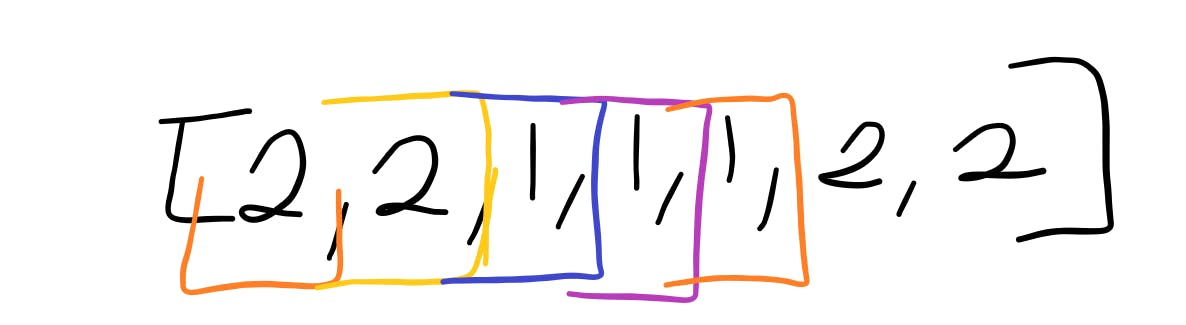
Algorithm:

is counter === 0; yes it is
- since the counter is 0, the current element becomes the majority element
- m = 1
is the value of m the same as the current element in the iteration
- yes; m = 1, while current num = 1
- so, go ahead and increment the counter variable

m = 1, counter = 1

Next element in the iteration - 2

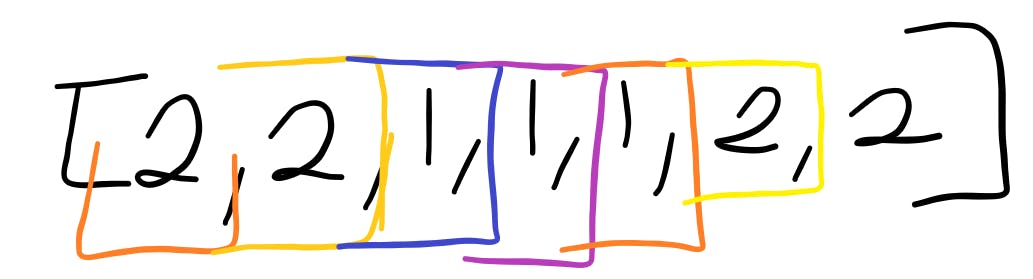
Algorithm:

is counter === 0; no it is 1
is the value of m the same as the current element in the iteration
- no; m = 1, while current num = 2
- so, go ahead and decrement the counter variable

m = 1, counter = 0

Last element in iteration - 2

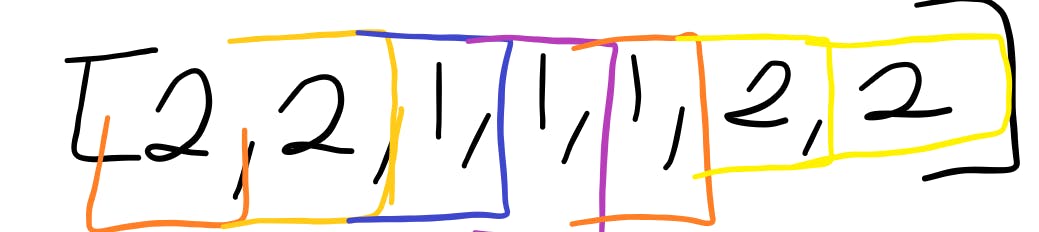
Algorithm:

is counter === 0; yes it is
- since the counter is 0, the current element becomes the majority element
- m = 2
is the value of m the same as the current element in the iteration
- yes; m = 2, while current num = 2
- so, go ahead and increment the counter variable

m = 2, counter = 1

This is the last element in the array; return m

Find the full code here

You can try this algorithm for a wide range of test cases, but as long as there is one element that is a majority, it would be the last man standing and cancel out the other occurrences.

If you would rather watch the video --> youtu.be/enVivn6eXJY

🍵 Happy coding

Leetcode 169: Majority element

data structures and algorithms

Table of contents

Understand the problem

Brute force approach

Complexity Analysis

Follow up

Boyer Moore's algorithm